If The System Has Infinitely Many Solutions It Is
Linear System Of Equations With Infinitely Many Solutions Youtube
If the system has infinitely many solutions it is. When you graph the equations both equations represent the same line. If the system has exactly one unique solution then it is independent. A system has a unique solution when it is consistent and the number of variables is equal to the number of nonzero rows.
Without graphing determine if the following system has no solution or infinitely many solutions. If the two lines have the same y-intercept and the slope they are actually the same exact line. If a consistent system has exactly one solution it is independent.
Linear System of Equations with Infinitely Many Solutions. Does it have a unique solution infinitely many solutions or no solutions. The three types of solution sets.
What does infinitely many solutions look like. A system of linear equations either has no solutions one solution or infinitely many solutions. For otherwise if it were consistent for every vector b it would necessarily be invertible again by the IM theorem but by assumption it is not.
For a system with infinitely many solutions it must be true that the coefficient matrix and the augmented matrix have the same rank and that this rank is less than the number of variables in the system. A system is consistent if it has a solution. The solution my be divided into two.
The system x y z 1. Has two equations and one variable but one solution. If two of the equations in a system of linear equations are inconsistent then the whole system is inconsistent.
If a consistent system has an infinite number of solutions it is dependent. In general ie.
Solved If The Following System Has Infinitely Many Chegg Com
Solved If The Following System Has Infinitely Many Chegg Com
Systems With No Solution Or Infinitely Many Solutions Ppt Download
Solved Solve The System If The System Has Infinitely Many Chegg Com
How To Solve This Linear System That Has Infinitely Many Solutions Socratic
Solved 1 Point If The Linear System Has Infinitely Many Chegg Com
Systems Of Linear Equations With Infinite Solutions Examples Expii
Number Of Solutions To System Of Equations Review Article Khan Academy
Solved If The Following System Has Infinitley Many Chegg Com
Warm Up Determine Whether Each System Has Zero One Or Infinitely Many Solutions One Infinitely Many Zero 3x Y 15 3x 2y 6 X 2y Ppt Download
One Solution No Solution Or Infinitely Many Solutions Consistent Inconsistent Systems Youtube
Two Systems Of Equations Are Given Below For Each Gauthmath
Solve 3x3 System With Elimination Infinitely Many Solutions Youtube
3 Variable System With Infinitely Many Solutions Youtube
Solved If The Following System Has Infinitely Many Chegg Com
If The System Of Equations 2x 3y 5 4x K Y 10 Has Infinitely Many Solutions Then Youtube
Linear Algebra Determine The Values Of A For Which The System Has No Solutions Exactly One Solution Or Infinitely Many Solutions Mathematics Stack Exchange
Solved If The Linear System Has Infinitely Many Solutions Chegg Com
Solve The Following System Of Linear Equations 2x1 2x2 Itprospt
Number Of Solutions To System Of Equations Review Article Khan Academy
Solved Find The Complete Solution Of The Linear System Or Chegg Com
Answered Solve The System State Whether The Bartleby
Solved Determine The Value Of H Such That The Following Chegg Com
1
Solved Solve The System If The System Has Infinitely Many Chegg Com
For How Many Values Of K Does The Given System Of Equations Have Infinitely Many Solutions Youtube
For A Real Number A If The System 1 A A 2 A 1 A A 2 A 1 X Y Z 1 1 1 Of The Linear Equations Has Infinitely Many Solutions Then 1 A A 2
If The System Of The Linear Equations Above Has Infinitely Many Solutions And C Is A Constant What Brainly Com
Solved Solve The System Or Show That It Has No Solution If Chegg Com
Solving Systems Of Equations Ppt Download
Solved For The Following Linear Systems Enter The Letter U Chegg Com
Answered Two Systems Of Equations Are Given Bartleby
Solve The System If The System Has Infinitely Many S Itprospt
Warm Up Tell Whether The System Has One Solution No Solution Or Infinitely Many Solutions Ppt Download
If The System Of Equations 2x 3y 7 A B X 2a B Y 21 Has Infinitely Many Solutions Then A A 1 B 5 B A 5 B 1 C A 1 B 5 D A 5 B 1
In The System Of Equations Above A And B Are Constants If The System Has Infinitely Many Youtube
A Unique Solution No Solution Or Infinitely Many Solutions Ax B Solutions Unique Linear System
Q12 Find C If The System Of Equations Cx 3y 3 C 0 Has 12x Cy C 0 Has
If A Pair Of Linear Equations Has Infinitely Many Solutions Then The Lines Representing Them Will Bea Parallelb Intersecting Or Coincidentc Always Intersectingd Always Coincidentcorrect Answer Is Option D Can You Explain This Answer Edurev
If The System Of Equations 2x 3y 7 2ax A B Y 28 H Scholr
Use Row Operations To Solve The System X Y Z 5 Itprospt
How Many Solutions Does A System Of Linear Equations Have If There Are At Least Two Video Khan Academy
If The System Of Equations 2x 3y 7 And A B X 2a B Y 21 Has Infinitely Many Solutions Then Sarthaks Econnect Largest Online Education Community
Solve 3x3 System Row Echelon Form Infinitely Many Solutions Youtube
Drag Each Pair Of Equations To Show If The System Has No Solutions One Solution Or Infinitely Many Brainly Com
For What Value Of K Will The Following Pair Of Linear Equations Have Infinitely Many Solutions Kx 3y K 3 012x Ky K 0 Mathematics Topperlearning Com S9dgqn55
Solved Two Systems Of Equations Are Given Below For Each Chegg Com
Infinitely Many Solutions Ppt Download
1
An equation can have infinitely many solutions when it should satisfy some conditions.
A system of linear equations either has no solutions one solution or infinitely many solutions. So if the coefficient matrix of a system of equations has determinant 0 then the system is either inconsistent or it has infinitely many solutions. Think of a real number bthat makes the system inconsistent and a real number bwhich makes the system have infinitely many solutions. If a consistent system has exactly one solution it is independent. The system x y z 1. The system of an equation has infinitely many solutions when the lines are coincident and they have the same y-intercept. Has three equations and two variables but infinitely many solutions. In other words theyre the same exact line. This algebra video tutorial explains how to determine if a system of equations contain one solution no solution or infinitely many solutions.
Meanwhile an inconsistent equation has no solution. For all vectors b will this system be inconsistent or will it have infinitely many solutions. If two of the equations in a system of linear equations are inconsistent then the whole system is inconsistent. If A x b and A 0 then A 1 exists so x A 1 b is the unique solution of the system. A system with intersecting lines is considered consistent because it has at least one solution and independent because it has exactly one solution. The system x y z 1. This type of equation is called a dependent pair of linear equations in two variables.
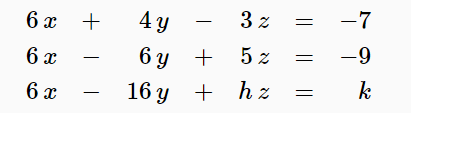
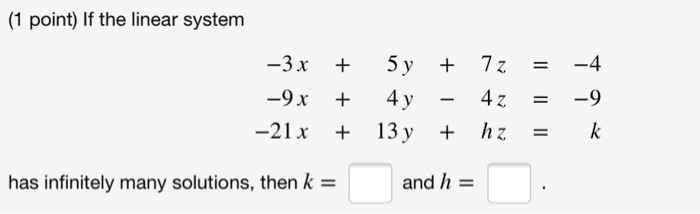
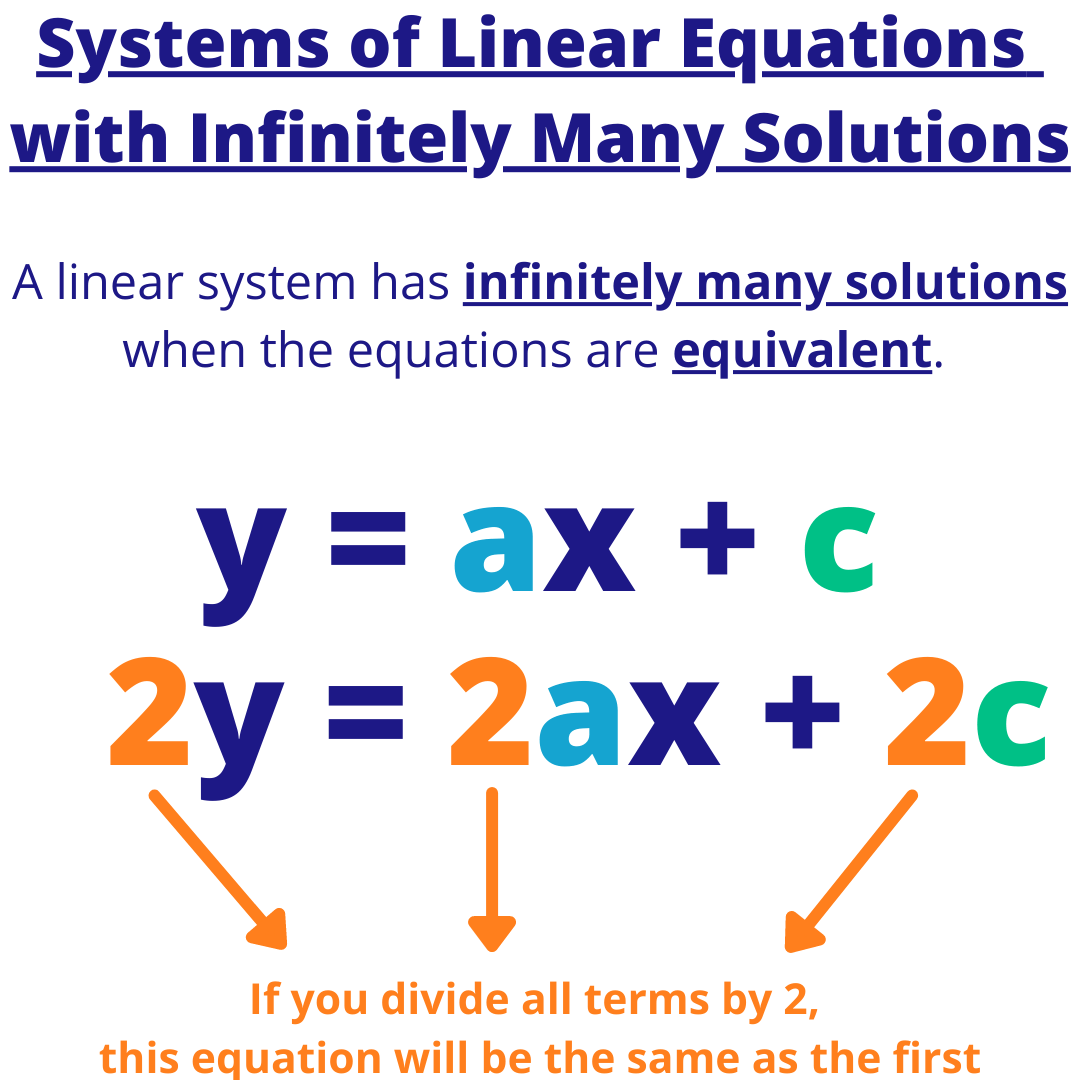
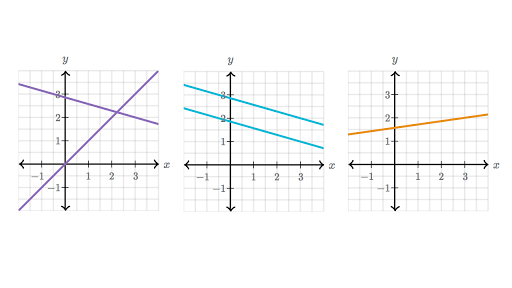
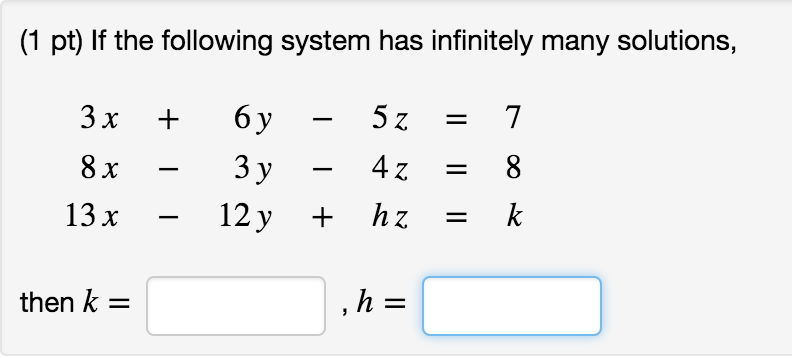
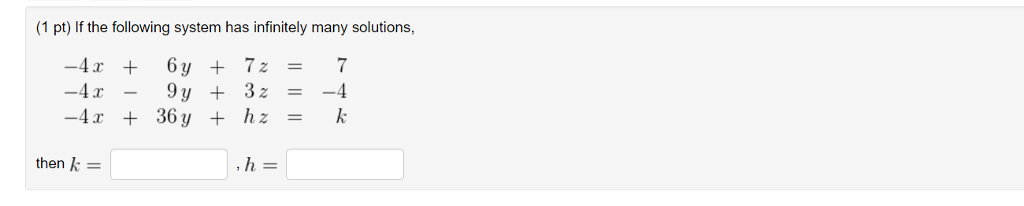
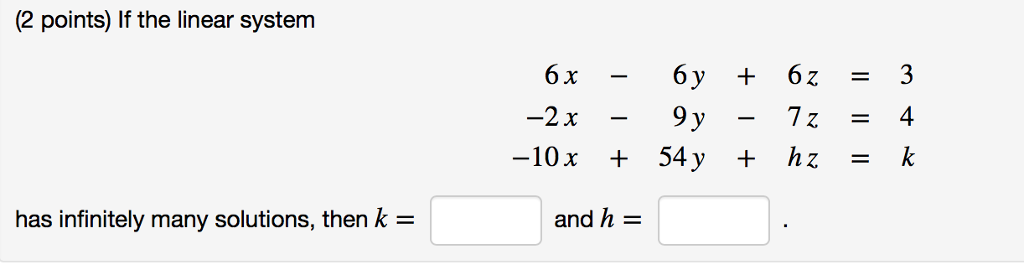
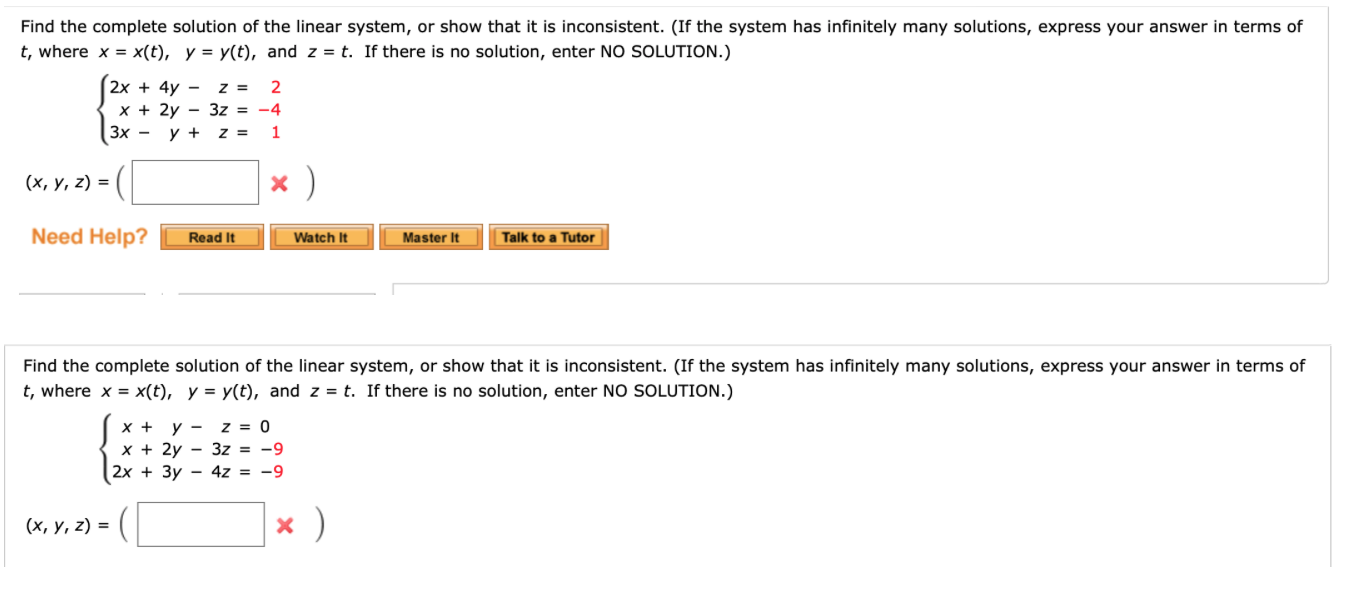
Post a Comment for "If The System Has Infinitely Many Solutions It Is"